The power of using a database to manage information comes from the use of advance index structures that make efficient searches to retrieve only the required information when it is actually needed. There are several different index structures available to people designing databases and with this page I hope to get people a guide on how to use these structure to there full potential.

When designing the indexes used within a database management systems (DBMS), there are a couple of special considerations that influence the finial design. Firstly, with the size of many databases, it would be too slow to create an index each and every time a search is required and therefore the indexes are maintained over the life of the data. Secondly, the nature of disk drives is that they are capable of holding vast amounts of information, but accessing the data can be slow and if the indexes requires many small reads from the disk, as a B-Tree or AVL tree would require, performance can be severely hampered so the indexes need to be page orientated. And lastly, when the indexes are used by many people - only the best will do, the indexes must be as efficient as possible by being self leveling, to maintain efficiency under all various circumstances at all times.

The B+-Tree Indexes

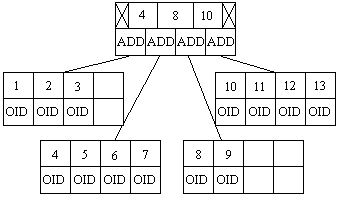
The most powerful of all database indexes is the B⁺-Tree index. It can use fixed or variable length keys and orders them in such a way as to allow multiple methods of searching, such as find first, last, greater than, less than as well as equal to. It is organized into pages that have much better read/write efficiency and it is also self-leveling. With its basic key design it can make use of most data formats, from integers, floating point, dates, text strings and so on.

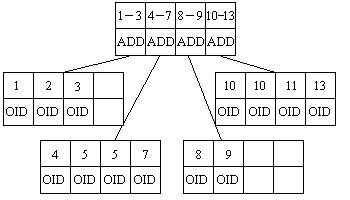
The B⁺-Tree is similar in design to be B-Tree but each node has more than one key value and two pointers, in fact each page of the B⁺-Tree normally contains about 50 or so key values that are sorted from smallest to largest. Within each key value within the index nodes is a pointer that has the reference to the next page below the node. The search first obtains the head node, searches through the list of keys until it finds the first key greater than the desired key than moves onto the next node, if no key is greater than the search key, then the last page is referenced. Once the leaf page at the bottom of the index is found, the corresponding ObjectID can be obtained and the search in complete.

When a new key is inserted into the B⁺-Tree index, the search finds if the desired position is free, then if there is not enough room to fit the new key within the page is broken up into two, filling each new page with half of the contents of the old and placing a new key into the new page. This creates a data structure that expands sideways rather than vertically like the humble B-Tree.

The Spatial Tree (S-Tree) Indexes

The S-Tree index is so called, as it is short for spatial indexes. Originally developed by Informix as a R-Tree index for grid searching in rectangular areas, it has now been further developed for 3 dimensional searches with cubes. S-Tree searches for any corresponding values that have some cross over area or volume and then builds a temporary index in memory for the standard read operations.

S-Tree has a very similar structural pattern as the B⁺-Tree indexes, but the key value in the above node does not separate those small to the left and larger to the right, S-Tree node values contain the bounding area for all the areas directly below. In this way, searching for all areas or volumes that have a cross region with the search key, a sub tree can be cancelled if none of its bounding values crosses the search key, thus giving it a O(n log(n)) build/creation efficiency rating.

The tree grows in a very similar manner as the B⁺-Tree, as an index key is placed into the best fitting leaf, if that leaf does not have enough space, the leaf is divided into two and a new key value is placed into the tree representing the new leaf.

One of the biggest differences between the B+Tree and the Spatial Index is that searching the Spatial Index can return more than one matching result and therefore a temporary index is created from the search query before any matching results are read from the database. Spatial and Token List indexes are special in the way that they are an index structure used to create an index, rather that being the index itself.

The Temporal Tree (T-Tree) Indexes

Temporal Tree Indexes are very much similar to Spatial Indexes except they use time quantities CODBPP::DATE and CODBPP:FILETIME, and are one dimensional which goes from start to finish. T-Tree Indexes will search for all over lapping time periods between the search quantities and the corresponding index fields.

The Structure of the T-Tree is identical to the spatial indexes and is searched in identical fashion.

The Token List Indexes

Token List Indexes are designed for the quick searching of full text queries. There are two types of token list indexes, first is the ASCII (8 bit characters) token list and second is the wide character (16 bits) token list.

The token list structure is like the Spatial Index as more than one matching result can be found by searching the structure, so a temporary index is created before any reads from the database can take places. The Token List in structure is very similar to a variable B⁺-Tree index that has buckets to store the many matching ObjectIDs per token.

This Token List index first breaks up the defined index fields into each separate token that it contains, for example the string "the lazy brown fox" would be broken up into four tokens:- the; lazy; brown; fox, each of these token would then be indexed and the ObjectID added to the matching bucket. Then the temporary index is created, the search only has to cross check each unique token and not the full text of each field in each object.

The Token List searches provides several different mechanisms for the search, firstly there are the Boolean logical operators: - and; or; xor; not; and (). Secondly there are token operators: - if a token is to contain a string, "A" or A; if a token is to start with a string " A"; if a token is to end with a string "A "; and lastly, is a token is to match a given string " A ". Where more advance search logic is required you are to implement this yourself, for example if you wanted a search "A near B", you would have to search "A and B" then read each result to cross check that A was in fact near B. This is because the Token List index does not provide this sort of searching abilities and the implementation would be the same if done within ObjectDatabase++ or not.

The Hash Indexes

Hash Indexes are some times used in a DBMS and fall into two groups - dynamic and static hashing. Static hashing is very powerful, but are usable only within a handful of applications, it also has the staggering search efficiency rating of O(1) and is used by ObjectDatabase++ to reference the ObjectIDs. It basically is an index array where the ObjectID points directly to a position in the array where the address for the object is located. However, static hashing is very limited in its application, holes can occur, only unique values can be used and the hash algorithm needs to be simple.

Dynamic hashing on the other hand is more flexible, but when it is created into a general algorithm for all situations the search efficiency rating drops to O(log(n)), which is the same as the trusty old B⁺-Tree index, but without the ability to search for the first, last, next, previous, greater than and less than. This is why many DBMS and ObjectDatabase++ do not offer dynamic hashing indexes.

Try today by freely downloading ObjectDatabase++ GUI Editor